In diesem Hauptseminar geht es darum ein visuell ansprechendes Bild zu erzeugen, in welchem ein mathematischer Inhalt dargestellt wird. Es folgen die von den Studierenden erzeugten Ergebnisse der vergangenen Semester.
Inhaltsverzeichnis
- Sommersemester 2021
-
Wintersemester 2017/18
- Theodora Sikioti und Vincent Degner: Das Dodekaplex
- Antonia Berger und Florian Volk: Zwillingsdodekaeder
- Jan Voggeneder und Sascha Zielke: Hyperbolische Pflasterungen
- Nils Otto und Patrick Halbritter: Die Weierstraß'sche p-Funktion
- Florian Bürger, Tobias Fix, Julian Kress und Ann-Kathrin Schmitt: Die Cartoide -- eine Kaustik
- Martin Pense: Julia- und Mandelbrodmengen
- Wintersemester 2016/17
- Wintersemester 2015/16
Sommersemester 2021
In Arbeit...
Wintersemester 2017/18
Theodora Sikioti und Vincent Degner: Das Dodekaplex
Aus regelmäßigen 3, 4, oder 5 Ecken kann man die fünf Platonischen Körper, den Tetraeder, Oktaeder, Ikosaeder, Wüfel und Dodekaeder herstellen. Um sich diese Figuren vorzustellen ist es natrülich von Nutzen sich ein 3-dimensionales Modell zu bauen, oder, wenn man gerade mal kein Werkzeug zur Hand hat kann man auch eine 2-dimensionale Zeichnung anfertigen.
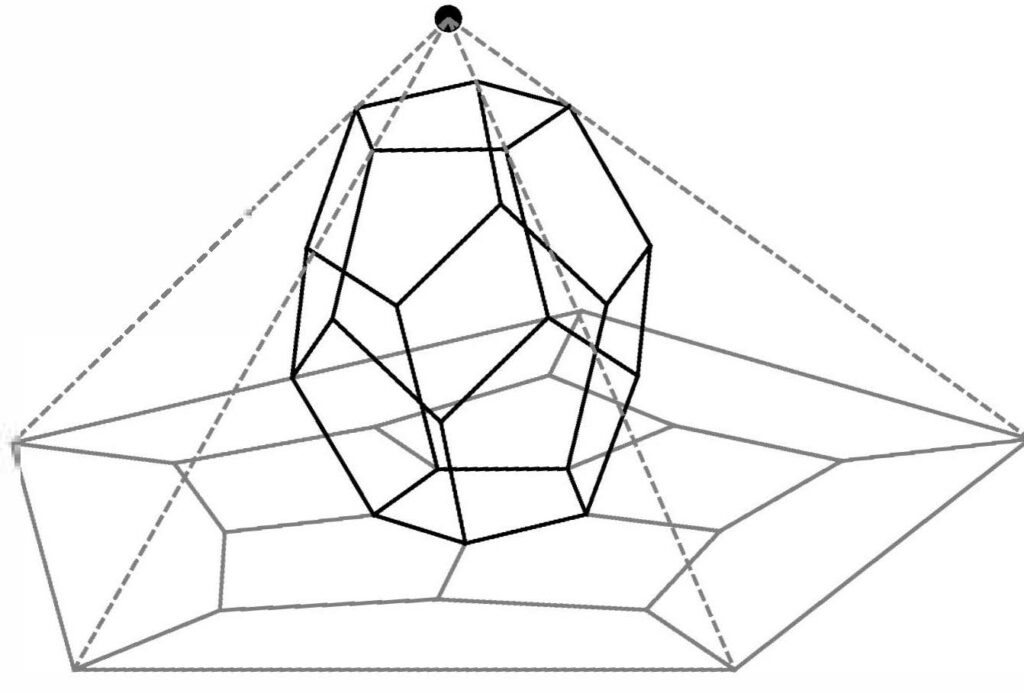
Am Beispiel des Dodekaeders ist dies in der kleinen nebenstehenden Grafik dargestellt, zusammen mit einer stereographischen Projektion, welche den Dodekaeder dann als Netz auf die Ebene abbildet. Wie man sieht besteht der Dodekaeder aus 12 (=\(\delta\omega\delta\epsilon\kappa\alpha\) auf altgriechisch) Fünfecken, wobei sich jeweils 3 dieser Fünfecke in einer Ecke treffen. Bei der Projetion werden diese Fünfecke (verzerrt) auf die Zeichenebene abgebildet (wo ist das oberste Fünfeck geblieben?).
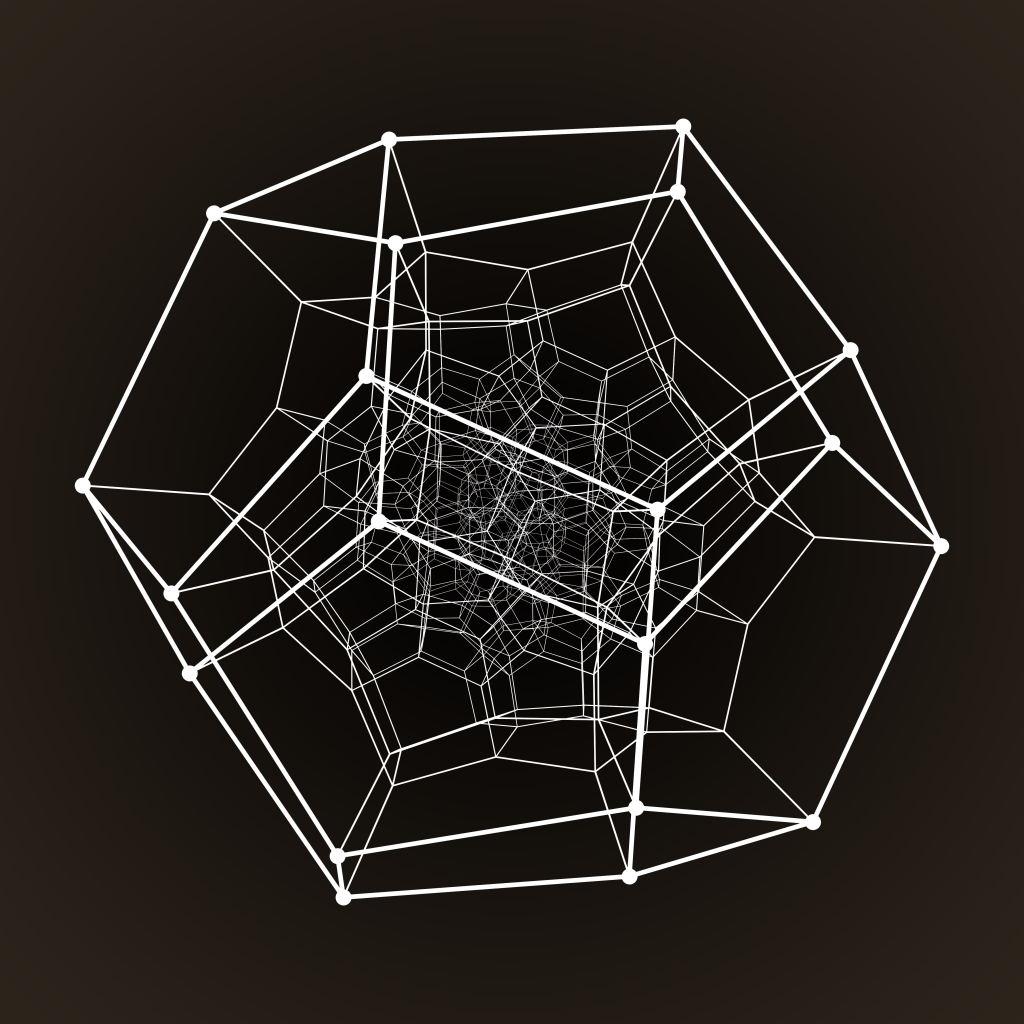
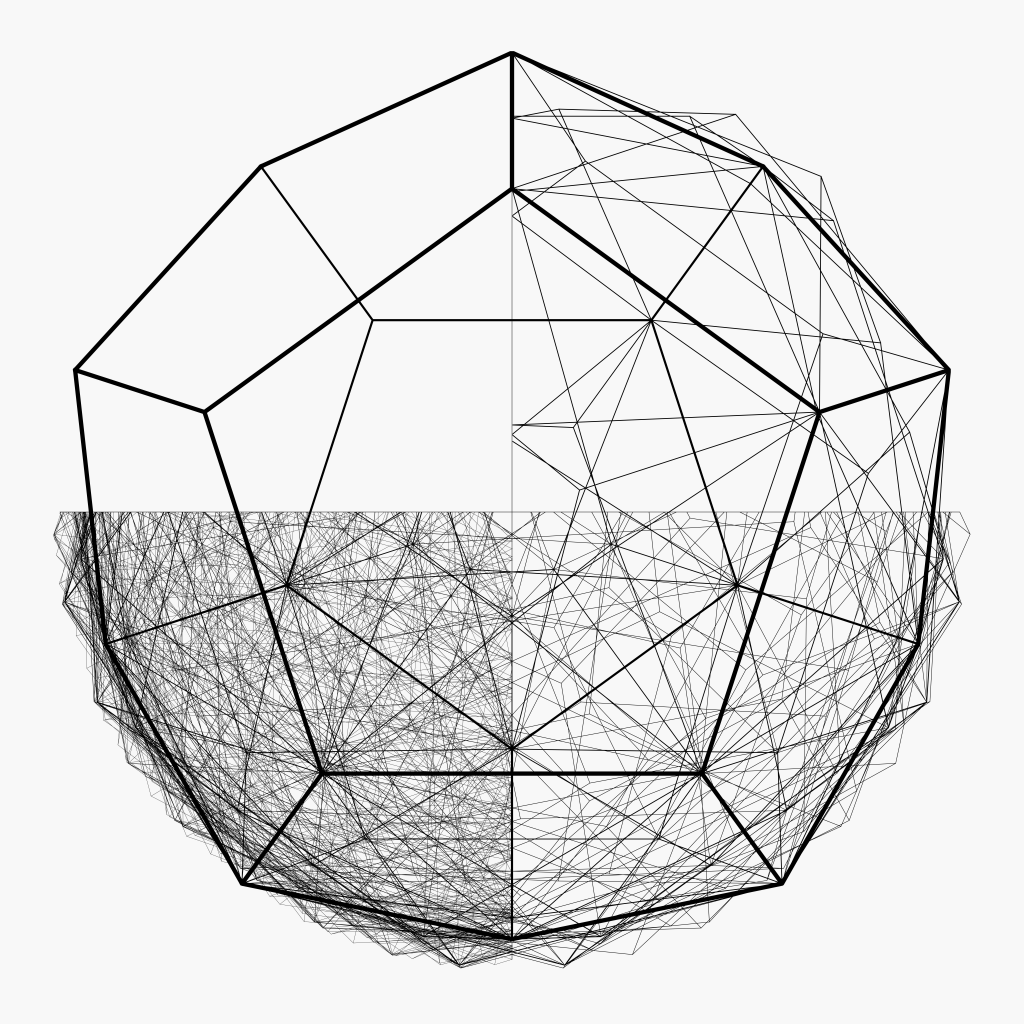
Das Dodekaplex entsteht indem man jeweils 3 Dodekaeder an einer Kante zusammenfügt. Das geht allerdings nur noch im vierdimensionalen Raum. Durch wiederholtes Hinzufgen weiterer Dodekaeder erhält man einen 4 Dimensionalen regulären Polyeder, der aus 120 (dreidimensionalen) Dodekaedern besteht. Er hat 600 Ecken 1200 Kanten und 720 Fünfecksflächen. Die große Grafik oben zeigt eine Darstellung des Dodekaplex, welche Ähnlich dem oben beschriebenen Netz des Dodekaeders gewonnen wurde, nur eben in einer Dimension höher.
Das Dodekaplex gehört zu den regelmäßigen (konvexe) Polytopen. Listet man die Anzahl der verschiedenen regel-mäßigen Polytope für die Dimensionen \(N \geq 2\) auf, ergibt sich die Zahlenreihe
\[
\infty, 5, 6, 3, 3, 3, 3, ...
\]
Die Dimensionen 2, 3 und 4 scheinen in dieser Hinsicht also besonders zu sein, da es in ihnen mehr regelmäßige Polytope gibt als in allen anderen Dimensionen.
Antonia Berger und Florian Volk: Zwillingsdodekaeder

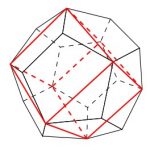
Ein Dodekaeder ist ein Körper, dessen Oberfläche nur aus regelmäßigen Fünfecken besteht. Insgesamt sind es zwölf Stück, von denen sich je drei an einer Ecke treffen. Er ist einer der fünf platonischen Körper. Ein anderer ist der Würfel. Wenn man sich den Dodekaeder genauer ansieht, stellt man fest, dass man in ihm mehrere Würfel findet. Einen davon zeigt nebenstehende Abbildung.
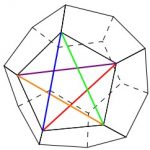
Geht man von einem Fünfeck des Dodekaeders aus und betrachtet dort eine feste Diagonale, so lassen sich genau acht Ecken des Dodekaeders finden, die einen Würfel bilden, der diese Diagonale als Kante hat.
Das geht genauso auch mit jeder anderen Diagonalen, die in der nebenstehenden Abbildungen dargestellt sind. Auf diese Weise lassen sich in einem Dodekaeder genau fünf verschiedene Würfel entdecke
n.
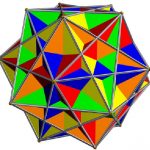
 Über jedem dieser Würfel können wir schließlich noch einen anderen Dodekaeder bilden. Dieser Prozess ist in der rechten Abbildung dargestellt. Der ursprüngliche Dodekaeder wird über einer beliebigen Würfelfläche um \(90^\circ\) gedreht. Einen auf diese Weise entstandenen Dodekaeder nennen wir \textbf{Zwillingsdodekaeder}. Startet man mit einem Dodekaeder und bildet über jedem der fünf Würfel den dazugehörigen Zwilling, so erhält man fünf Zwillingsdodekaeder. Von diesen kann man natürlich wieder die Zwillinge bilden -- und so weiter. Das Erstaunliche ist:
Über jedem dieser Würfel können wir schließlich noch einen anderen Dodekaeder bilden. Dieser Prozess ist in der rechten Abbildung dargestellt. Der ursprüngliche Dodekaeder wird über einer beliebigen Würfelfläche um \(90^\circ\) gedreht. Einen auf diese Weise entstandenen Dodekaeder nennen wir \textbf{Zwillingsdodekaeder}. Startet man mit einem Dodekaeder und bildet über jedem der fünf Würfel den dazugehörigen Zwilling, so erhält man fünf Zwillingsdodekaeder. Von diesen kann man natürlich wieder die Zwillinge bilden -- und so weiter. Das Erstaunliche ist:
Durch Wiederholung dieses Prozesses erhält man unendlich viele verschiedene Dodekaeder!
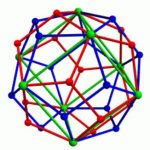
Die Eckpunkte all dieser Dodekaeder liegen auf einer Kugeloberfläche. Auf den beiden Postern sind die Dodekaeder mittels einer stereographischen Projektion in die Ebene projeziert worden. Ähnlich wie bei einer Landkarte wird dadurch alles etwas verzerrt. Während man auf dem einen Bild die Kanten aller Dodekaeder in ihrer Entwicklung bis zur vierten Stufe sieht, sind auf dem anderen Bild nur die Ecken dargestellt. Die dunkelsten Punkte gehören zum ursprünglichen Dodekaeder. Findest du alle Ecken, die zu einer der Seitenflächen gehören?
Jan Voggeneder und Sascha Zielke: Hyperbolische Pflasterungen
Dieses Bild zeigt eine hyperbolische \({3, 8}\) Pflasterung mit 14 Generationen, deren Fundamentalpolygon im Ursprung zentriert ist. Es besteht also aus hyperbolischen 3-ecken, von denen jeweils 8 in einer Ecke zusammentreffen.
Unter einer ebenen Geometrie versteht man Mengen von Punkten P und Geraden G, deren mögliche Lage untereinander durch spezifische Axiome bestimmt werden. In der uns vertrauten euklidischen Geometrie gibt es genau drei ver-schiedene reguläre Pflasterungen der Ebene, nämlich die Pflasterung mit Dreiecken, die Pflasterung mit Vierecken und die Pflasterung mit Sechsecken aus dem nebenstehenden Übersichtsbild.
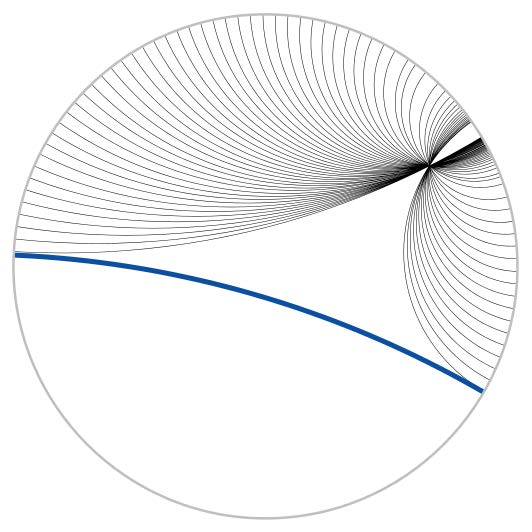
Ein weiteres Beispiel für eine Geometrie ist die hyperbolische Geometrie. Dort gibt es im Gegensatz zur euklidischen Geometrie zu jeder gegebenen Geraden \(g\) unendlich viele parallele Geraden, die durch einen Punkt \(a\) verlaufen, der nicht auf \(g\) liegt. Diese Geometrie kann nicht ohne Weiteres in der euklidischen Ebene dargestellt werden. Man benötigt ein Modell zur Betrachtung, hier das Poincaré-Kreisscheiben Modell. Dort werden hyperbolische Geraden als Kreisbögen dargestellt, die den Rand des Einheitskreises orthogonal schneiden. Die Nebenstehende Grafik zeigt die Familie der Paralellen zu der blauen Gerade durch einen Punkt.
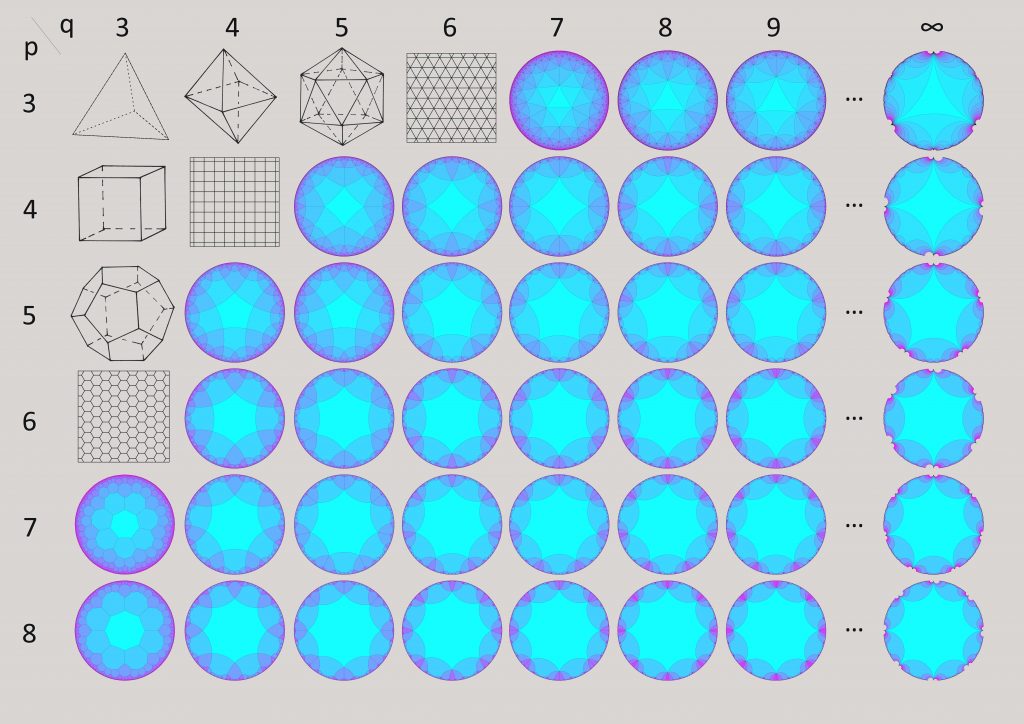
Eine reguläre Pflasterung der hyperbolischen Ebene ist nun eine lückenlose und überlappungsfreie Überdeckung durch gleichartige regelmäßige Polygone (d.h. alle Seiten sind gleich lang und alle Winkel zwischen den Seiten gleich groß) der hyperbolischen Ebene. Eine solche Pflasterung entsteht, indem man mit einem Fundamentalpolygon startet und dieses mit Hilfe der Isometrien Inversion am Kreis, Rotation und Translation der Poincaré-Kreisscheibe abbildet. Dabei sollen die Polygone der jeweils nächsten Generation an die äußeren Kanten der vorherigen Generation angelagert werden.
Eine Klassifizierung solcher Pflasterungen ist über das Schläfli-Symbol \(\{p, q\}\) möglich. Dabei gibt \(p\) die Anzahl der Ecken der einzelnen Polygone an und \(q\) die Anzahl der Polygone, die an jeder Ecke der Pflasterung zusammentreffen. Eine reguläre Pflasterung der hyperbolischen Ebene existiert für \(p\) und \(q\), genau dann wenn \((p − 2) · (q − 2) > 4\). Folglich existieren unendlich viele reguläre Pflasterungen der hyperbolischen Ebene wovon einige in der unteren Grafik, ergänzt durch die spharischen und ebenen Pflasterungen, dargestellt sind.
Nils Otto und Patrick Halbritter: Die Weierstraß'sche p-Funktion
Bereits Schüler lernen mit dem bekanntesten Vertreter, der (reellen) Sinusfunktion, periodische Funktionen kennen. Der Sinus behält seine Periodizität auch, wenn man ihn als Funktion in \(\mathbb{C}\) auffasst, auch für \(z \in \mathbb{C}\) gilt:
\[
sin(z) = sin(z + 2k\pi), k \in \mathbb{Z}
\]
Wir bezeichnen ein \(\omega \in \mathbb{C}\) als Periode der Fkt. \(f\), wenn \(f(z) = f(z+\omega) \forall z\) im Definitionsbereich. Die Menge aller Perioden von \(f\), \(Per(f)\), bildet eine additive Gruppe. \(Per(sin(z)) = \mathbb{Z}2\pi\) ist zyklisch, ein weiteres Beispiel dieser Form ist \(Per(e^z) = \mathbb{Z}2\pi i\)
Diese prominenten Beispiele werfen die Frage auf, ob es (neben konstanten Funktionen \(c\), \(Per(c) = \mathbb{C}\)) überhaupt periodische Funktionen gibt, deren Periodengruppe eine andere Form als \(\mathbb{Z}\omega\) besitzt. Tatsächlich lässt sich zeigen, dass es Funktionen gibt, deren Periodengruppe die Form \(\mathbb{Z}\omega_1 + \mathbb{Z}\omega_2\) besitzt, wobei \(\omega_1, \omega_2\) linear unabhängig sind, wenn man \(\mathbb{C}(\cong \mathbb{R}^2)\) als \(\mathbb{R}\)-Vektorraum auffasst. Dann spannen sie nämlich ein Gitter auf. Der berühmteste Vertreter dieser sogenannten \glqq doppelt-periodischen\grqq Funktionen ist die Weierstraß'sche \(\wp\)-Funktion. Zu dem Gitter \(\Gamma = \mathbb{Z}\omega_1 + \mathbb{Z}\omega_2\) definiert man sie wie folgt:
\[
\wp(z) = \frac{1}{z^2} + \sum \limits_{\omega\in \Gamma\backslash {0}} \frac{1}{(z-\omega)^2} - \frac{1}{\omega^2}
\] Diese Reihe ist für alle \(z\in \mathbb{C}\backslash\Gamma\) definiert und konvergiert. Die \(\wp\)-Funktion ist außerdem differenzierbar, und ihre Ableitung \(\wp'(z) = \sum \limits_{\omega\in \Gamma} \frac{2}{(z-\omega)^3}\) ist ebenfalls eine doppelt-periodische Funktion zum selben Periodengitter \(\Gamma\). Mit \(\wp\) und \(\wp'\) haben wir im Prinzip alle doppelt-periodischen Funktionen beschrieben. Jede doppeltperiodische Funktion lässt sich nämlich als rationale Funktion in \(\wp\) und \(\wp'\) darstellen.
Diese Reihe ist für alle \(z\in \mathbb{C}\backslash\Gamma\) definiert und konvergiert. Die \(\wp\)-Funktion ist außerdem differenzierbar, und ihre Ableitung \(\wp'(z) = \sum \limits_{\omega\in \Gamma} \frac{2}{(z-\omega)^3}\) ist ebenfalls eine doppelt-periodische Funktion zum selben Periodengitter \(\Gamma\). Mit \(\wp\) und \(\wp'\) haben wir im Prinzip alle doppelt-periodischen Funktionen beschrieben. Jede doppeltperiodische Funktion lässt sich nämlich als rationale Funktion in \(\wp\) und \(\wp'\) darstellen.
Das obige Bild zeigt die Weierstraß'sche \(\wp\)-Funktion für das Gitter \(\Gamma = \mathbb{Z} + \mathbb{Z}i\). Zur Verständnis der Darstellung betrachtet man die nebenstehende kleine Grafik. Für jeden Punkt auf der komplexen Ebene betrachtet man das Bild unter \(wp\), und färbt den Punkt entsprechend der Farbe des Bildpunkts auf der kleinen Grafik ein.
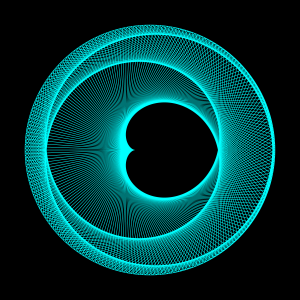
Florian Bürger, Tobias Fix, Julian Kress und Ann-Kathrin Schmitt: Die Cartoide -- eine Kaustik


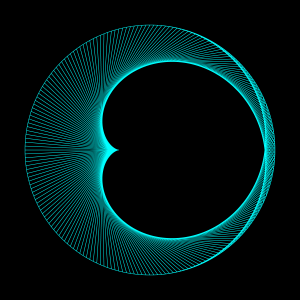
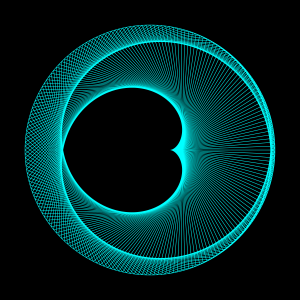
Kaustiken sind physikalischen Phänomene, die jeder im Alltag beobachten kann. Es handelt sich dabei um die Brennlinien, die durch Lichtbrechung oder Lichtreflexion entstehen. Erstere bezeichnet man als Diakaustiken, zweiter als Katakaustiken. Die beiden folgenden Bilder stellen eine Katakaustik in einer Kaffeetasse und eine Diakaustik im Wasser dar. Etwas mathematischer fomuliert sind Kaustiken Hüllkurven (auch: Enveloppe), die durch eine Schar von Geraden entstehen, die man als Lichtstrahlen auffassen kann. Die Kaustik wird dabei in jedem ihrer Punkte genau einmal von der Geradenschar (Lichtstrahlen) tangential berührt. Das Aussehen einer Kaustik kann von der Position der Lichtquelle abhängen.Liegt die Quelle im Unendlichen, handelt es sich um parallel einfallendes Licht. Andernfalls geht man von einer radialen, punktförmigen Lichtquelle aus.
Auf dem untenstehenden Bilder repräsentiert die erste Entwicklungsstufe (erste Darstellung in der Reihe) eine Kaustik, die durch Reflexion der Lichtstrahlen am Kreis entsteht, wobei sich die Lichtquelle im Unendlichen befindet. Diese Art Kaustik nennt man Kardioide (sog. Kaeetassenkaustik). Die weiteren kleinen Bilder zeigen die Lichtstrahlen nach der zweiten, dritten und vierten Reflexion. Im großen Bild oben ist die Kaustik nach der 10ten Reflexion dargestellt.
Martin Pense: Julia- und Mandelbrodmengen
Wir betrachten zu jeder komplexen Zahl \(c\) die Funktion \(f_c(z)=z^2+c\) auf der komplexen Zahlenebene. Wenden wir \(f_c\) auf einen Startwert $z_0$ an, setzen dann das Ergebnis wieder in \(f_c\) ein und wiederholen diesen Vorgang immer wieder, so erhalten wir eine Folge
\[ z_0, f_c(z_0), f_c(f_c(z_0)), f_c(f_c(f_c(z_0))),\ldots \]
die betragsmäßig entweder beliebig groß wird oder beschränkt bleibt.
Es sei \(K_c\) die Menge der Startwerte, für die die zu \(f_c\) gehörende Folge beschränkt
ist. Diese Teilmenge der komplexen Zahlenebene \(K_c\) nennt man die ausgefüllte Juliamenge zum Wert \(c\). Die Juliamenge \(J_c\) der Funktion \(f_c\) ist dann der Rand von \(K_c\). Die Mandelbrotmenge \(M \subseteq \mathbb{C}\) ist definiert als die Menge der Parameter \(c\), für die \(0\)
in \(K_c\) enthalten ist. Das kleine Bild links zeigt die ausgefüllte Juliamenge zum Parameter \(c = -0,7+0,1i\), rechts daneben ist die Mandelbrotmenge dargestellt Es bestehen einige Verbindungen zwischen der Mandelbrotmenge und den Juliamengen \(J_c\) von denen im obigen großen Bild eine dargestellt wird: um einige Punkte \(c\) innerhalb
Es bestehen einige Verbindungen zwischen der Mandelbrotmenge und den Juliamengen \(J_c\) von denen im obigen großen Bild eine dargestellt wird: um einige Punkte \(c\) innerhalb
und außerhalb der Mandelbrotmenge \(M\) sind verkleinert die zugehörigen Mengen \(K_c\) abgebildet.
Ist \(c \in M\), so ist \(J_c\) zusammenhängend, ansonsten zerfällt die Juliamenge in total
unzusammenhängenden Cantorstaub. Der Rand der Mandelbrotmenge fungiert dabei wie ein Wörterbuch alle jener Juliamengen: Für Werte \(c\) auf dem Rand hat der Rand der Mandelbrotmenge im Kleinen eine änliche Gestalt wie die entsprechende Juliamenge.
Wintersemester 2016/17
Marius Kling und Sebastian Hassemer: Schmidtsche Kreiskonfigurationen
Möbiustransformationen sind Abbildungen der Form
\[ f(z) = \frac{a z+b}{c z + d},\]
mit Parametern \(a, b, c\) und \(d\), wobei \(ad - bc=1\) ist. Dabei fasst man \(f\) als Abbildung der komplexen Zahlenebene auf sich selbst auf. Diese besteht aus sogenannten komplexen Zahlen, also Zahlen der Art \(z = x+i\cdot y\), wobei die imaginäre Einheit \(i = \sqrt{-1}\) ist und \(x\), sowie \(y\) aus den reellen Zahlen sind. Setzt man reelle Werte für \(z\) ein, so liegen die Punkte von \(f(z)\) auf einem Kreis (bzw. einer Geraden). Anschaulich bedeutet dies, dass die reelle Achse zu einem Kreis gebogen wird. Erlaubt sind dabei auch komplexe Zahlen für die Parameter, so bildet
\[ f(z) = \frac{1-zi}{z-i} \]
die reelle Gerade, wie in der Zeichnung angedeutet, auf einen Kreis ab.
Variiert man nun die Koeffizienten über alle ganzen komplexen Zahlen, d.h. solche \(z=x+i\cdot y\) für die \(x\) und \(y\) aus den ganzen 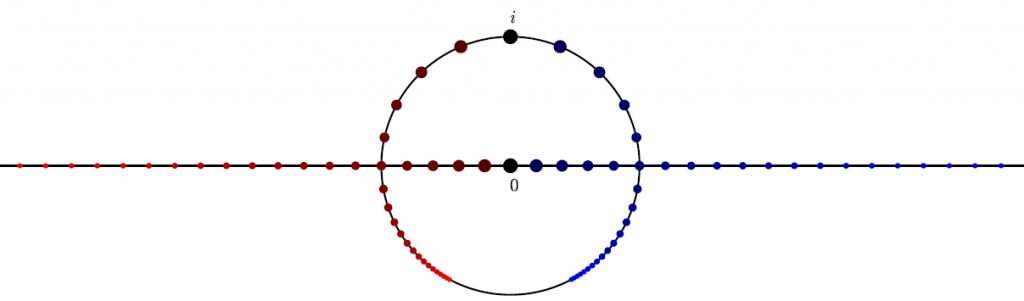 Zahlen sind, und zeichnet für alle diese Möbiustransformationen den oben beschriebenen Kreis, so erhält man die nach Schmidt benannte Kreiskonfiguration.Die nebenstehende Grafik zeigt einen gedrehten Ausschnitt der komplexen Zahlenebene mit eben dieser Struktur.
Zahlen sind, und zeichnet für alle diese Möbiustransformationen den oben beschriebenen Kreis, so erhält man die nach Schmidt benannte Kreiskonfiguration.Die nebenstehende Grafik zeigt einen gedrehten Ausschnitt der komplexen Zahlenebene mit eben dieser Struktur.
Neben den schon von Gauß untersuchten ganzen komplexen Zahlen, gibt es in der Zahlentheorie noch weitere wichtige Zahlenbereiche. Wählt man die Parameter aus einem von diesen, erhält man durch ähnliches Vorgehen ebenfalls Kreiskonfigurationen. Allein am Aussehen dieser Konfigurationen lassen sich wichtige Eigenschaften der Zahlenbereiche ablesen.
Jan Disselhoff und Simon Schweitzer: Schottky Gruppen
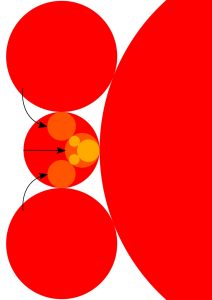 Wir beginnen mit 4 Kreisen. Das Äußere des einen Kreises bilden wir auf das Innere des gegenüberliegenden ab. Wie in der nebenstehenden Grafik illustriert, wird der rechts stehende große Kreis quasi um den kleinsten roten Kreis gestülpt. Dabei werden die drei roten Kreise, wie durch die Pfeile angedeutet, verkleinert. Wiederholt man diesen Abbildung nochmal, so entstehen die hellorangenen Kreise. Abbildungen dieser Art, die Kreise auf Kreise abbilden, nennt man Möbiustransformationen. Sie sind benannt nach dem deutschen Mathematiker August Ferdinand Möbius (1790 --- 1868) und sind ein wichtiger Bestandteil der Theorie der kompexen Funktionen.
Wir beginnen mit 4 Kreisen. Das Äußere des einen Kreises bilden wir auf das Innere des gegenüberliegenden ab. Wie in der nebenstehenden Grafik illustriert, wird der rechts stehende große Kreis quasi um den kleinsten roten Kreis gestülpt. Dabei werden die drei roten Kreise, wie durch die Pfeile angedeutet, verkleinert. Wiederholt man diesen Abbildung nochmal, so entstehen die hellorangenen Kreise. Abbildungen dieser Art, die Kreise auf Kreise abbilden, nennt man Möbiustransformationen. Sie sind benannt nach dem deutschen Mathematiker August Ferdinand Möbius (1790 --- 1868) und sind ein wichtiger Bestandteil der Theorie der kompexen Funktionen.
Auf die eben beschriebene Art und Weise erhält man also für zwei gegenüberliegende Kreise eine Möbius\-trans\-formation und ihre Umkehrung, insgesamt also 4 Abbildungen. Wendet man diese vier Abbildung in allen möglichen Reihenfolgen immer und immer wieder auf die Anfangskonfiguration von 4 Kreisen an, so entstehen durch diese ins Unendliche fortgeführten Wiederholungen fraktalähnliche Strukturen. Unter bestimmten Bedingungen vereinigen sich die durch diesen unendlichen Prozess entstehenden Kreise zu einer geschlossenen Linie von faszinierender Schönheit.
Die Gesamtheit der möglichen Kompositionen der 4 Möbiustransformationen bilden zusammen eine sogenannte Schottkygruppe. Dies ist im Allgemeinen eine überabzählbar unendliche Gruppe. Das nebenstehende Poster visualisiert also wie diese Gruppe als Ganzes auf der Ebene operiert.
Manuel Krummeck, Tamara Nutz und Kim Vosen: Nullstellen von Littlewoodpolynomen
Für dieses feurige Bild betrachten wir ganz besondere Funktionen: die Littlewood-Polynome (LWP). Diese haben die allgemeine Form:
\[
f(x)= \pm 1 \pm x \pm x^{2} \pm ... \pm x^{n}
\]
Man erkennt hier bereits ihre Besonderheit: alle Vorfaktoren von $x$ sind entweder \(1\) oder \(-1\). Wir betrachten nun beispielsweise \(f(x)= 1 + x + x^{2}\). Dieses hat den Grad 2, entsprechend der höchsten Potenz von \(x\). Die \(pq\)-Formel liefert die beiden Nullstellen von \(f(x)\)
\[ \textstyle x_{1,2} = - \frac{1}{2} \pm \sqrt{(\frac{1}{2})^2-1} = - \frac{1}{2} \pm \frac{\sqrt{-3}}{2} .
\textstyle x_{1,2} = - \frac{1}{2} \pm \sqrt{(\frac{1}{2})^2-1} = - \frac{1}{2} \pm \frac{\sqrt{-3}}{2} .
\]
In den reellen Zahlen besitzt \(f(x)\) demnach keine Nullstelle, da wir unter der Wurzel eine negative Zahl, die \(-3\), steht. Fügt man zu den reellen Zahlen die imaginäre Einheit \(i\) dazu, so erhält man die komplexen Zahlen. Diese Einheit \(i\) hat folgende Eigenschaft: \(i^2 = -1\). Mit diesem Trick kann man aus negativen Zahlen die Wurzel ziehen und erhalten wir die beiden komplexen Nullstellen:
\[
\textstyle - \frac{1}{2} + \frac{\sqrt{3}}{2} i \text{ und } - \frac{1}{2} - \frac{\sqrt{3}}{2} i
\]
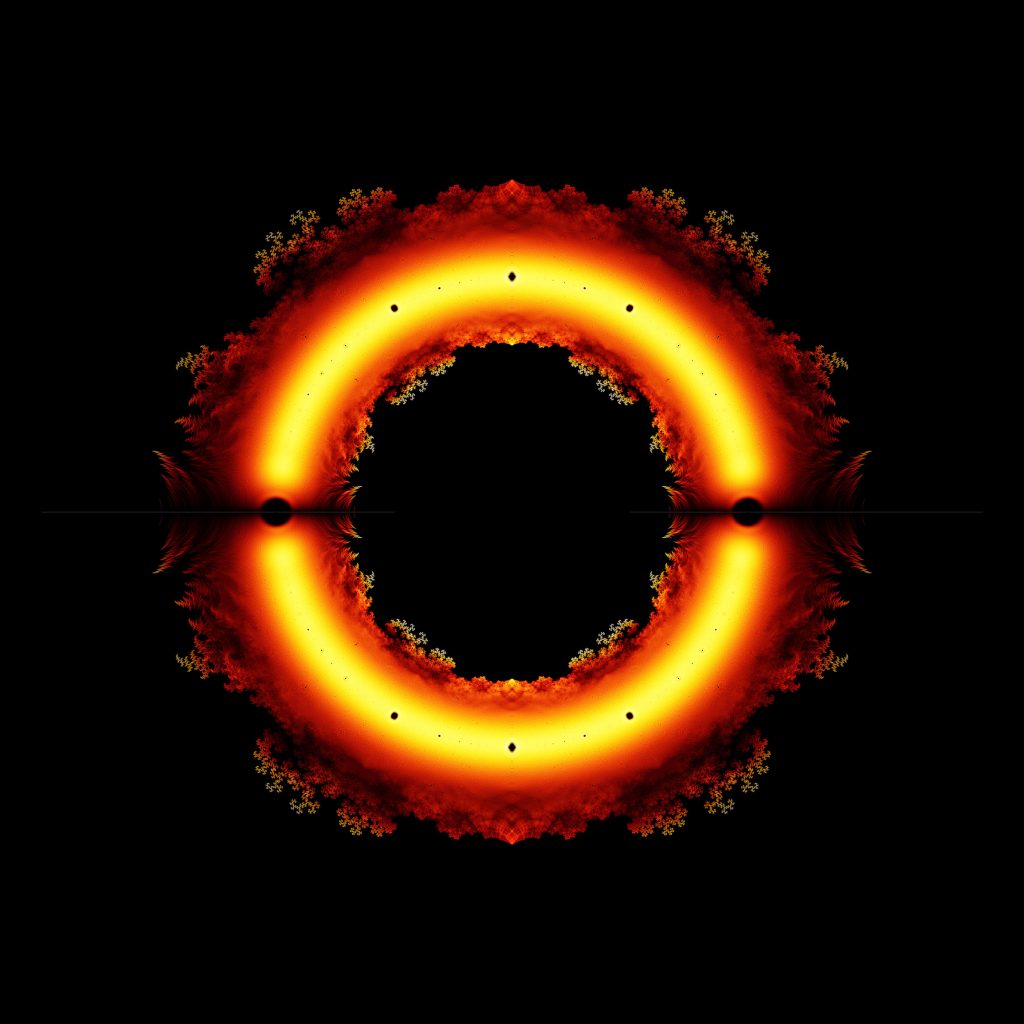
Nun kann man die Nullstellen auf der entstehenden komplexen Zahlenebene abtragen, wobei das \((- \frac{1}{2})\) in der Zahlenebene nach rechts und das \((\frac{\sqrt{3}}{2} i)\) nach oben abgetragen werden. Aber zwei Punkte ergeben noch lange kein Bild! Zeichnet man aber alle 90 Millionen Nullstellen aller LWP vom Grad 22, das heißt \(f(x) = x^{22} \pm x^{21} \pm ... \pm 1\), in die Zahlenebene ein, dann erhält man damit den Ring und die schönen drachenartigen Muster. Um die Färbung zu erhalten, wurden die Punkte, die sehr oft als Nullstelle auftreten viel heller gezeichnet, als solche die nur selten als Nullstelle auftreten. Dabei werden weiße Punkte bis zu 500.000fach getroffen, wie beispielsweise der helle Ring und die Spitzen der Muster am Rand der Nullstellenmenge.
Interessanterweise, ähneln die Randmuster stark den Drachenkurven. Ein Zusammenhang ist vermutet, mathematisch aber noch nicht ganz erforscht. Vielleicht hat dieses Poster Ihr Interesse geweckt, diesen Zusammenhang näher zu erforschen?

Färbt man die Nullstellenmenge der Littlewood-Polynome
mit den Farben des Regenbogens, so entsteht ein neues Bild. Hierzu wurde jedem
Littlewood-Polynom, wie nebenstehend angedeutetdet eine Farbe des Spektralfarbbereichs zugeordnet. Die Polynome vererben dann ihre Färbung an ihre zugehörigen Nullstellen.
Das untenstehende Poster zeigt einen Ausschnitt des unteren rechten Quadranten der
Littlewood Nullstellenmenge. Fällt Ihnen im Kreisinnern etwas auf? Benachbarte
Nullstellen haben die gleiche Farbe! Doch warum ist dies so? Dies möchten wir an einem
Beispiel illustrieren:
Betrachten wir dafür die gelbe Drachenkurve im Zentrum des Posters um den Punkt
\((0{,}43; -0{,}48)\). Dies sind einige Nullstellen der Funktionen, die dem gelben
Farbbereich zugeordnet sind, also:
\[
f(x) = 1 - x - x^2 - ... - x^8 + x^9 - x^{10} \pm x^{11} \pm ... \pm x^{21}
\pm x^{22}
\]
 Setzt man dieses \(x = (0{,}43; -0{,}48)\) in \emph{alle} Littlewoodpolynome mit der obigen
Setzt man dieses \(x = (0{,}43; -0{,}48)\) in \emph{alle} Littlewoodpolynome mit der obigen
Färbung ein, so erhalten wir für die Funktionswerte \(f(x)\) die links abgebildete kleine Drachenkurve. Darüber hinaus ist deren gelber Teil nahezu deckungsgleich mit den entsprechend gefärbten (gelben) Bereich der Littlewoodnullstellen um den Punkt \(x\) im nebenstehenden Poster.
Variiert man diesen \(x\)-Wert leicht, so ändert sich die Drachenkurve
minimal, wie auch die Anordnung der Punkte in der Littlewoodschen Nullstellenmenge.
Wintersemester 2015/16
Sven Partenheimer und Daniel Schisch: Complex
 In der nebenstehenden Abbildung ist der Graph der Funktion
In der nebenstehenden Abbildung ist der Graph der Funktion
\[f(x) = \frac{1}{x^{5}} \cdot \frac{x^{11}-1}{x-1} \]
dargestellt. An dem Graphen sind, abgesehen von der \(y\)-Achse als vertikaler Asymptote, nicht viele Eigenschaften dieser
Funktion ablesbar.
Dies ändert sich, wenn man statt des reellen Zahlenstrahls die komplexe Zahlenebene \(\mathbb{C}\) betrachtet, deren Elemente sich als \(x=a+ib\), wobei \(a\) und \(b\) reelle Zahlen sind, schreiben lassen. Diese komplexe Zahl \(x\) entspricht dann dem Punkt der Zeichenebene mit Koordinaten \((a,b)\). Man rechnet mit komplexen Zahlen wie üblich unter Verwendung der Regel \(i^2=-1\). Beim Versuch den Graphen einer komplexen Funktion zu realisieren stößt man allerdings auf das Problem, dass dazu 4 Dimensionen nötig sind.
Eine Lösung dieses Darstellungsproblems wird auf dem ausgestellten Poster gezeigt. Die Idee dabei ist es, den Funktionswert \(f(x)\) nicht nach oben abzutragen, sondern durch eine Farbe zu kennzeichnen: Jeder komplexen Zahl wird zunächst, abhängig von der Richtung bezüglich des Koordinatenursprungs, eine Farbe gemäß nebenstehender Farbskala zugeordnet. Nun färbt man die Zahl \(x\) der komplexen Zahlenebene mit der Farbe des Bildpunktes \(f(x) \in \mathbb{C}\) ein.
 Tut man dies für die oben beschriebene Funktion \(f(x)\) -- und fügt noch sinnvoll Schattierungen hinzu -- so ergibt sich das auf dem Poster dargestellte Bild. Am fünffachen Durchlaufen des Farbkreises in umgekehrter Reihenfolge ist nun die fünffache Polstelle am Nullpunkt, welche vom Faktor \(1/x^5\) stammt, deutlich zu erkennen. Ebenso deutlich lassen sich die 10 kreisförmig angeordneten, einfachen Nullstellen ausmachen. Ausgenommen die 1, liegen diese gerade auf den Eckpunkten eines dem Einheitskreises einbeschriebenen, regelmäßigen 11-Ecks. Es sind gerade die Nullstellen des 11. Kreisteilungspolynoms
Tut man dies für die oben beschriebene Funktion \(f(x)\) -- und fügt noch sinnvoll Schattierungen hinzu -- so ergibt sich das auf dem Poster dargestellte Bild. Am fünffachen Durchlaufen des Farbkreises in umgekehrter Reihenfolge ist nun die fünffache Polstelle am Nullpunkt, welche vom Faktor \(1/x^5\) stammt, deutlich zu erkennen. Ebenso deutlich lassen sich die 10 kreisförmig angeordneten, einfachen Nullstellen ausmachen. Ausgenommen die 1, liegen diese gerade auf den Eckpunkten eines dem Einheitskreises einbeschriebenen, regelmäßigen 11-Ecks. Es sind gerade die Nullstellen des 11. Kreisteilungspolynoms
\[
\frac{x^{11}-1}{x-1}=1+x+x^2+x^3+x^4+x^5+x^6+x^7+x^8+x^9+x^{10},
\]
welches der zweite Faktor unserer Funktion \(f(x)\) ist. Und dass am Rande des Bildes der Farbkreis noch fünf weitere Male durchlaufen wird, ist auch kein Zufall.
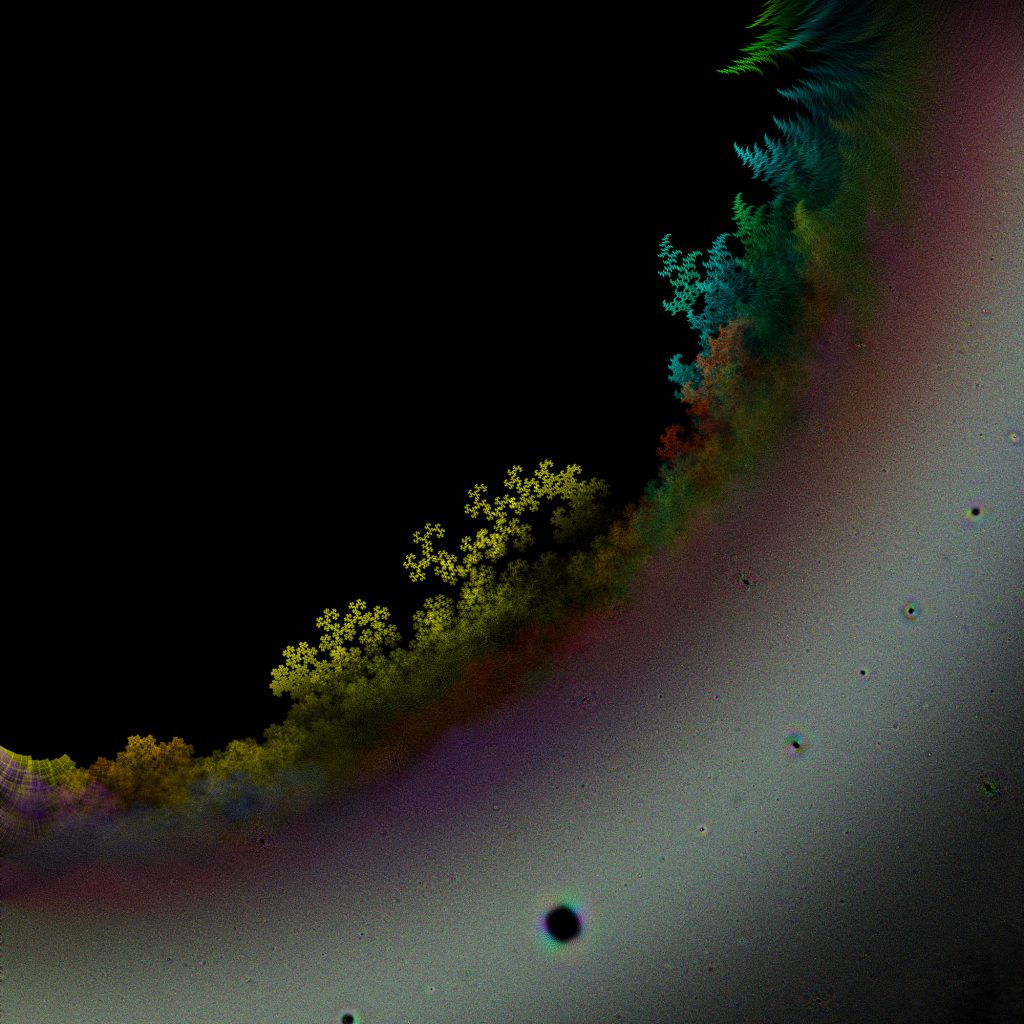
Nina Kissinger und Timo Stockhausen: Zwillingsdrachenkurve
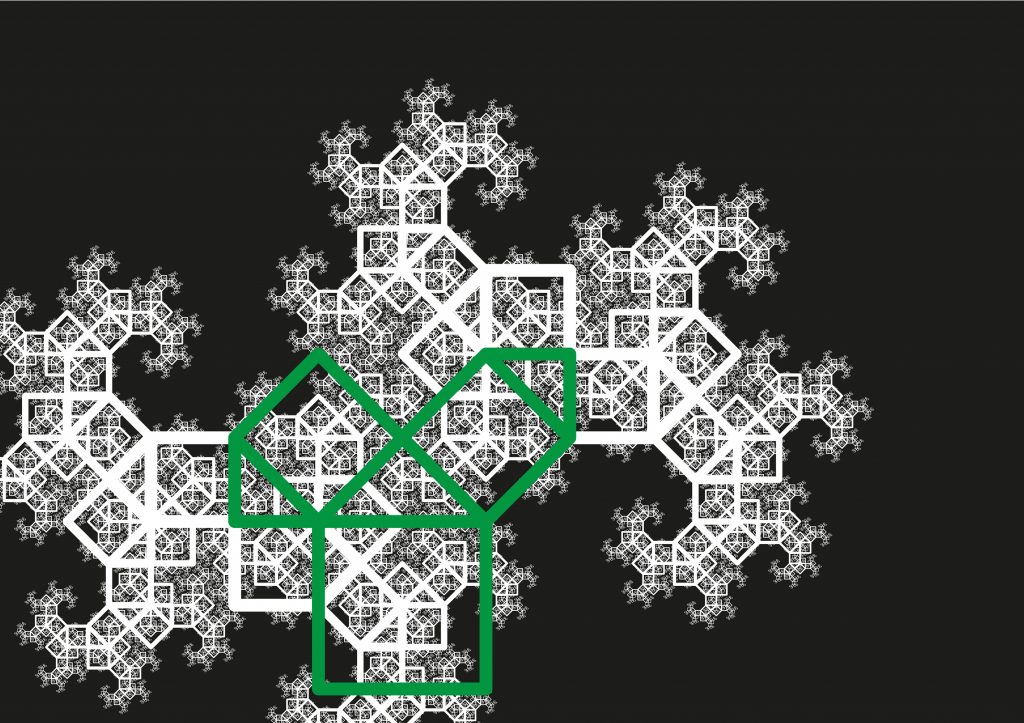
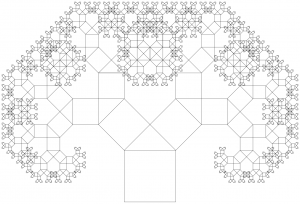 Die nebenstehende Grafik stellt den Baum des Pythagoras dar, der zur den Fraktalen zählt. Den Ursprung der Figur bildet die bekannte Darstellung zum Satz des Pythagoras, die aus einem rechtwinkligen Dreieck und den an den Kanten anliegenden Quadraten mit entsprechender Kantenlänge besteht.
Die nebenstehende Grafik stellt den Baum des Pythagoras dar, der zur den Fraktalen zählt. Den Ursprung der Figur bildet die bekannte Darstellung zum Satz des Pythagoras, die aus einem rechtwinkligen Dreieck und den an den Kanten anliegenden Quadraten mit entsprechender Kantenlänge besteht.
Der Baum entsteht nun aus dem Häuschen mit Dach (das untere Quadrat mit dem rechtwinklige Dreieck als Dach), indem man auf die Dachseiten das Häuschen entsprechend verkleinert immer wieder aufsetzt. Nach 10 Wiederholungen diese Prozesses entsteht die rechts dargestellte Figur.
 Variiert man diesen Prozess ein wenig, indem man auf der rechten Dachseite das Häuschen wie üblich aufsetzt, auf der linken Dachseite das Häuschen aber um 90 Grad nach links gedreht aufgesetzt, so erhält man man 15 Wiederholungen das auf dem Poster dargestellte Gebilde. Die dabei entstehende Randkurve wird interessanterweise wiederum durch ein anderes Fraktal angenähert: den sogenannten Zwillingsdrachen. Dieser entsteht aus einer Dopplung der Drachenkurve und ist in der kleinen Grafik rechts dargestellt.
Variiert man diesen Prozess ein wenig, indem man auf der rechten Dachseite das Häuschen wie üblich aufsetzt, auf der linken Dachseite das Häuschen aber um 90 Grad nach links gedreht aufgesetzt, so erhält man man 15 Wiederholungen das auf dem Poster dargestellte Gebilde. Die dabei entstehende Randkurve wird interessanterweise wiederum durch ein anderes Fraktal angenähert: den sogenannten Zwillingsdrachen. Dieser entsteht aus einer Dopplung der Drachenkurve und ist in der kleinen Grafik rechts dargestellt.
Die Drachenkurve selbst ist eine raumfüllende Kurve und bildet sich über den unten abgebildeten Prozess. Diese Drachenkurve kann man auch durch Papierfalten erhalten, indem man einen Streifen Papier wiederholt in der Mitte faltet und danach wieder so auffaltet, dass die Falze einen rechten Winkel bilden. Probieren Sie es aus.
Irina Alberg und Laura Herbst: Teilbarkeit im Pascalschen Dreieck
Das Pascalsche Dreieck entsteht, indem man entlang der Ränder eines Dreiecks die 1 schreibt und dann das Dreieck so auffüllt, dass jeder Eintrag gerade die Summe der direkt darüber stehenden Einträge ist. Das Pascalsche Dreieck spielt in vielen Bereichen der Mathematik eine Rolle und es versteckt sich viel Interessantes darin (einfach mal die Zeilen summieren und schauen, was rauskommt).
In der obenstehenden Grafik ist das Pascalsche Dreieck von der 0-ten bis zur 10-ten Zeile dargestellt. Dabei wurden alle ungeraden Einträge grau und alle geraden Einträge weiß hinterlegt. Das entstehende Muster erinnert an das sogenannte Sierpińksi-Dreieck.
Der Entstehungsprozess des Sierpińksi-Dreiecks ist auf der linken Hälfte des Posters zu sehen. Die blauen Bereiche entsprechen dann wie oben angedeutet genau den ungeraden Zahlen. Die Figur auf der rechten Hälfte des Posters entsteht auf ähnliche Art und Weise, indem die nicht durch 3 teilbaren Zahlen des Pascalschen Dreiecks grün gekennzeichnet werden.
Beim Überschneiden der beiden Figuren entsteht ein neues Muster, das man als diejenigen Einträge des Pascalschen Dreiecks deutet, die nicht durch 3 oder nicht durch 2 teilbar sind. Die freigelassenen Bereiche entsprechen folglich denjenigen Zahlen, die durch 6 teilbar sind. Es erscheint also eine bildliche Darstellung des sogenannten Chinesischen Restsatzes, der besagt: Sind \(a\) und \(b\) zwei Zahlen, die keinen gemeinsamen Teiler haben, so wird eine Zahl genau dann vom Produkt \(ab\) geteilt, wenn sowohl \(a\) als auch \(b\) diese Zahl teilen.
Julia Gemmer und Björn Eder: Eisensteinprimzahlen
Eine Primzahl ist eine positive ganze Zahl, welche sich nicht als Produkt von kleineren Zahlen schreiben lässt. So sind zum Beispiel \(6=2\cdot 3\) oder \(100=5 \cdot 5 \cdot 2 \cdot 2\) keine Primzahlen, und \(3,5,7\) oder \(101\) sind Primzahlen. Die Bedeutung von Primzahlen rührt von der Tatsache, dass sich jede ganze Zahl eindeutig als Produkt von Primzahlen schreiben lässt: 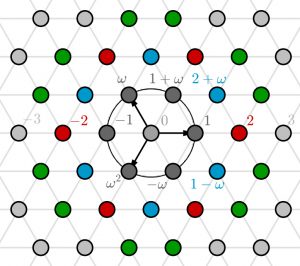 Dies ist der Fundamentalsatz der Arithmetik. Primzahlen sind also die kleinsten Bauteile, die Atome, der ganzen Zahlen. Die Erforschung von Primzahlen birgt viele einfach zu stellende Fragen, deren Antwort zum Teil bis heute noch nicht gefunden werden konnten.
Dies ist der Fundamentalsatz der Arithmetik. Primzahlen sind also die kleinsten Bauteile, die Atome, der ganzen Zahlen. Die Erforschung von Primzahlen birgt viele einfach zu stellende Fragen, deren Antwort zum Teil bis heute noch nicht gefunden werden konnten.
Erweitert man die ganzen Zahlen um eine weitere ,,Zahl'' $\omega$, welche die Rechenregel \((1+ \omega)=-\omega^2\) befolgt, so erhält man die \textbf{Eisensteinzahlen}. Bildlich kann man sich diese wie nebenstehend als Punkte in der Ebene vorstellen. Addiert werden Eisensteinzahlen wie Vektoren in der Ebene. Man kann Eisensteinzahlen aber auch multiplizeren: Zum Beispiel gilt
\[
(2+\omega)\cdot(1-\omega) =2-2\omega+\omega-\omega^2 =2-\omega+(1+\omega) =3
\]
unter Verwendung der Rechenregel \(-\omega^2=(1+ \omega)\) für die mysteriöse Zahl \(\omega\). Diese Rechnung zeigt, dass die Primzahl 3 in den Eisensteinzahlen in das Produkt \(3=(2+\omega) \cdot (1-\omega)\) zerfällt, also dort gar keine Primzahl mehr ist! Tatsächlich geht dies auf verschiedene Arten und Weisen -- alle möglichen echten Primteiler von 3 sind in der Grafik blau dargestellt. Die Teiler der 7 sind in grün dargestellt.
Das dunkle Poster zeigt die Primzahlen in den Eisensteinzahlen. Die roten Punkte gehören dabei zu den Primzahlen der ganzen Zahlen, wie zum Beispiel der 2 oder 5, die in den Eisensteinzahlen immer noch Primzahlen sind. Die weißen Punkte sind also die wirklich neuen Eisensteinprimzahlen, also diejenigen, die es in den ganzen Zahlen noch nicht gibt. Die auffällige 6-er Symmetrie kommt durch Multiplikation mit den 6 Einheiten \(1,-1,\omega,-\omega,\omega^2,-\omega^2\) zustande, welche im kleinen Bild dunkelgrau dargestellt sind.
Das helle Poster zeigt die Primzahlen in dem Zahlkörper \(\mathbb{Q}[\sqrt{3}]\). Der Vergleich der beiden Bilder illustriert die Unterschiede zwischen imaginären und reellen Zahlkörpern